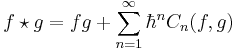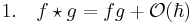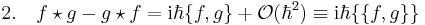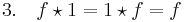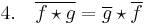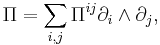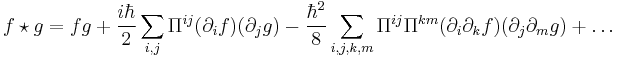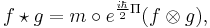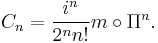Moyal product

In mathematics, the Moyal product, named after José Enrique Moyal, is perhaps the best-known example of a phase-space star product: an associative, non-commutative product, ∗, on the functions on ℝ2n, equipped with its Poisson bracket (with a generalization to symplectic manifolds below). This particular star product is also sometimes called Weyl-Groenewold product, as it was introduced by H. J. Groenewold in 1946, in a trenchant appreciation[1] of Weyl quantization —Moyal actually appears to not know about it in his celebrated paper,[2] and in his legendary correspondence with Dirac, as adduced in his biography.[3] (The paradoxical popular naming after Moyal, utilized in this stub, appears to have emerged only in the 1970s, in homage to his flat phase-space quantization picture.)

Contents

Definition

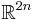The product (for smooth functions f and g on \mathbb R^{2n} takes the form

f\star g = fg %2B \sum_{n=1}^{\infty} \hbar^{n} C_{n}(f,g)

where each 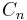C_n is a certain bidifferential operator of order n with the following properties. (See below for an explicit formula).

1.\quad f\star g = fg %2B \mathcal O(\hbar)

(Deformation of the pointwise product) — implicit in the definition.

2. \quad f\star g-g\star f = \mathrm i\hbar\{f,g\} %2B \mathcal O(\hbar^2) \equiv \mathrm i\hbar \{\{f,g\}\}

(Deformation of the Poisson bracket, called Moyal bracket.)

3. \quad f\star 1=1\star f=f

(The 1 of the undeformed algebra is also the identity in the new algebra.)

4. \quad \overline{f\star g} = \overline{g}\star \overline{f}

(The complex conjugate is an antilinear antiautomorphism.)

Note that, if one wishes to take functions valued in the real numbers, then an alternative version eliminates the 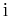\mathrm i in condition 2 and eliminates condition 4.

If one restricts to polynomial functions, the above algebra is isomorphic to the Weyl algebra 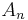A_n , and the two offer alternative realizations of Weyl quantization of the space of polynomials in n variables (or, the symmetric algebra of a vector space of dimension 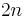2n).

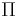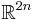To provide an explicit formula, consider a constant Poisson bivector \Pi on \mathbb R^{2n} :

\Pi=\sum_{i,j} \Pi^{ij} \partial_i \wedge \partial_j,

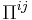where \Pi^{ij} is just a complex number for each i,j.

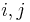The star product of two functions f and g can then be defined as

f\star g = fg %2B \frac{i\hbar}{2} \sum_{i,j} \Pi^{ij} (\partial_i f) (\partial_j g) - \frac{\hbar^2}{8} \sum_{i,j,k,m} \Pi^{ij} \Pi^{km} (\partial_i \partial_k f) (\partial_j \partial_m g) %2B \ldots

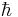where \hbar is the reduced Planck constant, treated as a formal parameter here.

A closed form can be obtained by using the exponential,

f\star g = m \circ e^{\frac{i\hbar}{2} \Pi}(f \otimes g),

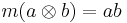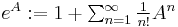where m is the multiplication map, m(a\otimes b) = ab, and the exponential is treated as a power series, \textstyle e^A�:= 1 %2B \sum_{n=1}^{\infty} \frac{1}{n!} A^n.

That is, the formula for 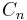C_n is

C_n = \frac{i^n}{2^n n!} m \circ \Pi^n.

As mentioned, often one eliminates all occurrences of 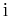\mathrm i above, and the formulas then restrict naturally to real numbers.

Note that if the functions f and g are polynomials, the above infinite sums become finite (reducing to the ordinary Weyl algebra case).

On manifolds

On any symplectic manifold, one can, at least locally, choose coordinates so as make the symplectic structure constant, by Darboux's theorem; and, using the associated Poisson bivector, one may consider the above formula. For it to work globally, as a function on the whole manifold (and not just a local formula), one must equip the symplectic manifold with a flat symplectic connection.

More general results for arbitrary Poisson manifolds (where the Darboux theorem does not apply) are given by the Kontsevich quantization formula.

Examples

A simple explicit example[4] of the construction and utility of the ∗-product (for the simplest case of a two-dimensional euclidean phase space) is given in the article on Weyl quantization. Every correspondence prescription between phase space and Hilbert space, however, induces its own proper ∗-product.

References

  1. ^ H.J. Groenewold, "On the Principles of elementary quantum mechanics", Physica,12 (1946) pp. 405-460.
  2. ^ J.E. Moyal, "Quantum mechanics as a statistical theory", Proceedings of the Cambridge Philosophical Society, 45 (1949) pp. 99-124.
  3. ^ Ann Moyal, "Maverick Mathematician: The Life and Science of J.E. Moyal", ANU E-press, 2006, http://epress.anu.edu.au/maverick_citation.html
  4. ^ C. Zachos, D. Fairlie, and T. Curtright, "Quantum Mechanics in Phase Space" ( World Scientific, Singapore, 2005) ISBN 978-981-238-384-6 .